标准正态分布表怎么使用目录
标准正态分布表怎么使用

标准正态分布表使用指南
1. 确定均值和标准差
在使用标准正态分布表之前,首先需要确定数据的均值(μ)和标准差(σ)。这两个参数是正态分布的核心参数,它们决定了数据分布的形状和范围。在确定均值和标准差之后,即可计算Z分数。
2. 查找对应的z值
Z分数是根据观测值和均值的差异计算的分数。要使用标准正态分布表,需要查找对应的Z分数。通常,Z分数可以通过以下公式计算:
Z = (X - μ) / σ
其中,X是观测值,μ是均值,σ是标准差。根据已知的μ和σ,代入观测值X进行计算,即可得到Z分数。
3. 使用累积分布函数
标准正态分布表提供了Z分数的累积分布函数值。累积分布函数表示的是在某个Z分数以下或以上的概率。通过查找对应的Z分数,可以找到对应的累积分布函数值。这个值表示观测值在正态分布中的位置。
4. 解释结果
根据查找到的累积分布函数值,可以解释观测值在正态分布中的位置和概率。例如,如果查找到的累积分布函数值为0.67,则表示观测值位于正态分布曲线下方0.67的概率密度。这有助于了解观测值的相对位置和概率。
5. 进行区间估计
标准正态分布表还可以用于进行区间估计。通过查找对应的Z分数范围,可以计算出在该范围内的概率区间估计。这对于假设检验、置信区间等方面非常重要。例如,如果要检验某变量的95%置信区间,可以通过查找Z分数的两个临界点来计算相应的置信区间范围。
6. 进行假设检验
标准正态分布表在假设检验中具有重要作用。通过计算样本均值与已知均值的Z分数,可以判断样本均值是否显著不同于已知均值。根据查找到的累积分布函数值,可以计算出相应的p值,从而判断假设检验的结果。
7. 用于相关性分析
标准正态分布表在相关性分析中也有应用。例如,在回归分析中,可以通过标准正态转换将自变量或因变量转换为标准正态分布的形式,从而更好地进行线性回归分析。这有助于消除数据的尺度效应,使得变量之间的关系更加线性化。
8. 注意事项
在使用标准正态分布表时,需要注意以下几点:
确保数据符合正态分布的假设。在进行转换之前,应该检查数据是否呈现正态分布的形状特征,如钟形曲线、无异常值等。
理解累积分布函数的含义和局限性。累积分布函数表示的是在某个Z分数以下或以上的概率,但并不能提供具体的概率值。因此,解释结果时应根据具体需求选择合适的解释方式。
熟练掌握查表技巧和精度要求。查表需要准确选择对应的Z分数,以确保查找到的累积分布函数值是准确的。在使用表格时,应根据实际情况调整查找精度。
标准正态分布表是如何使用的?
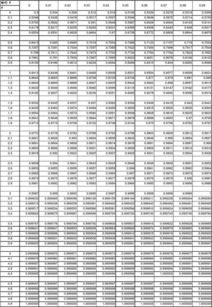
标准正态分布表的使用:针对于X
